MinCutPool: 이론편1 (MinCutPool: Understanding the Theory 1)

MinCutPool: 이론편1 (MinCutPool: Understanding the Theory 1)

MinCutPool은 복잡한 그래프에서 주요한 node를 추출하고자 한 여러 시도들 중 하나입니다. 일반적으로 node 추출은 graph를 matrix로 표현한 뒤 고유값 분해를 통해 핵심 node를 결정하는 spectral clustering(SC) 방법을 활용합니다. 하지만 고유값 분해 과정의 계산 복잡도가 높아 (\(O(N^3)\)) scalability issue가 있습니다. 최근 gradient descent 알고리즘을 활용하여 복잡도를 \(O(N^2)\)이나 \(O(N)\)까지 줄이는 연구가 있었습니다(Han & Filippone, 2017). 인공신경망을 이용한 연구도 진행되어 Autoencoder를 활용해 Laplacian matrix(Degree matrix - Adjacency matrix)의 i번째 행을 주요한 eigenvector들의 i번째 component에 연결시키는 작업도 이루어졌습니다(Tian et al., 2014). (Laplacian matrix에 대한 설명은 이 링크를 클릭하세요.)

본 논문에서는 eigenvector를 활용해야 하는 SC의 단점을 해소하면서 graph topology와 node의 feature를 기반으로 node를 clustering하는 방법론을 제시합니다. 이제부터 이론에 대해서 알아봅시다.

\[\begin{aligned} \bar{\mathbf{X}} &= \mathrm{GNN}(\mathbf{X},\tilde{\mathbf{A}};\mathbf{\Theta_{\mathrm{GNN}}}) \\ \mathbf{S} &= \mathrm{softmax}(\mathrm{MLP}(\bar{\mathbf{X}};\Theta_{\mathrm{MLP}})) \end{aligned}\]

\(\bar{\mathbf{X}}\)는 MP(Message passing, 하나의 graph neural layer 층으로 생각하면 됨)들을 통과하여 얻어진 node representation matrix입니다. \(\bar{\mathbf{X}}\)를 multi-layer perceptron(MLP, basic한 인공 신경망)과 softmax에 연달아 통과시켜 cluster assignment matrix \({\mathbf{S}}\)를 얻습니다. 이때 \(\Theta_{\mathrm{GNN}}\)와 \(\Theta_{\mathrm{MLP}}\)는 훈련 가능한 파라미터입니다. \(\mathbf{S}\)는 \([N \times K]\) 행렬으로 i번째 행에 node i가 각 cluster에 속할 확률을 담고 있습니다. \(\mathbf{S}\)가 softmax를 통과하는 과정에서 \(\mathbf{S}\)의 원소 \(\mathbf{s}_{ij}\)는 \(\mathbf{s}_{ij}\in [0,1]\)를 만족합니다. 그리고 \(\mathbf{S}\mathbf{1}_K=\mathbf{1}_N\)가 성립하게됩니다. (\([N \times K] \times [K \times 1]=[N \times 1]\), N개의 node, K개의 cluster)

그래프의 예시와 함께 확인해보겠습니다. 아래는 9개의 node로 이루어진 그래프와 그 인접행렬입니다.

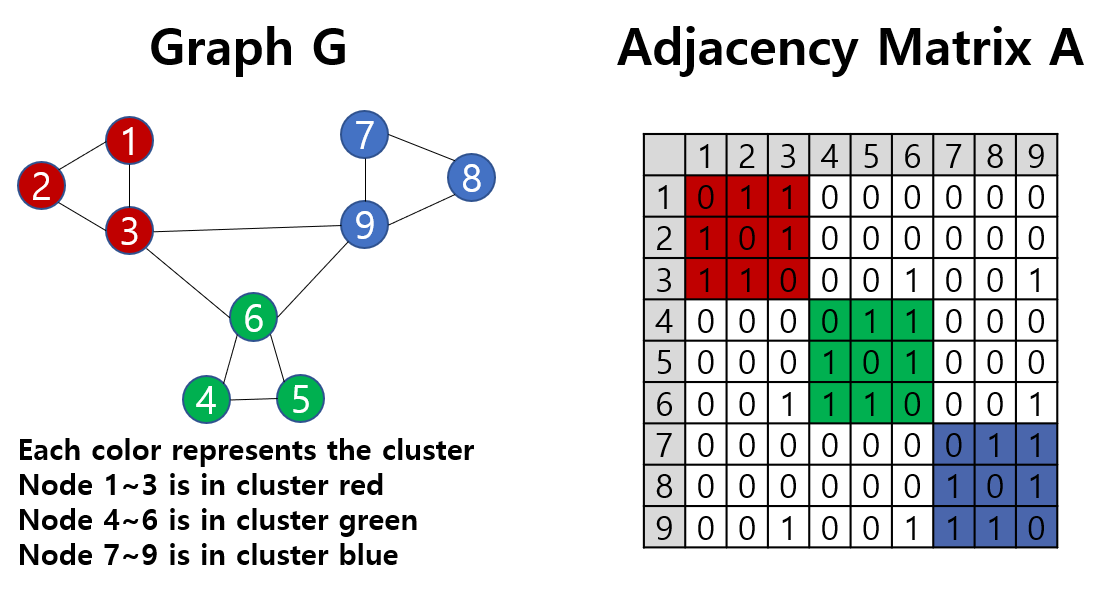
이 그래프의 최적 클러스터가 각각 적색, 녹색, 청색이라고 가정해봅시다. 그러면 최적 cluster 구성을 담은 행렬 \(\mathbf{C}\)를 표기할 수 있습니다. 그리고 \(\mathbf{C}\mathbf{1}_K=\mathbf{1}_N\)가 됨을 보일 수 있습니다.

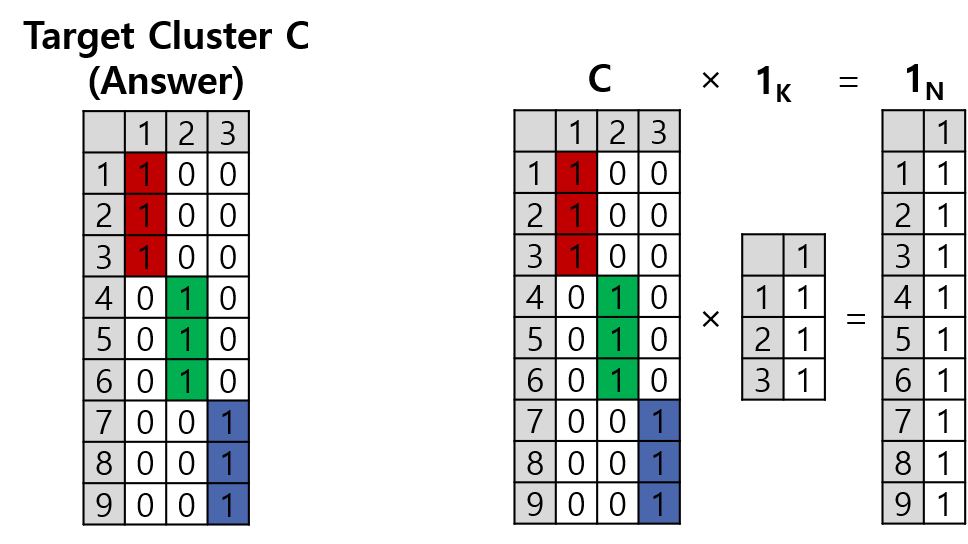
최적 cluster(정답)가 아닌 예측 결과 행렬 \(\mathbf{S}\)에서도 \(\mathbf{S}\mathbf{1}_K=\mathbf{1}_N\)는 성립합니다. \(\mathbf{S}\)의 i 번째 행은 i 번째 node가 각 cluster에 속할 확률을 나타냅니다.

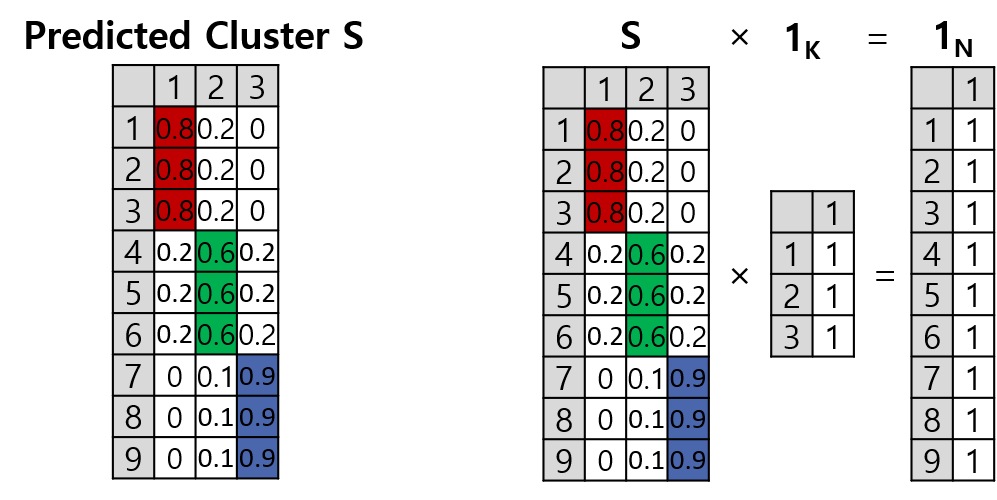
행렬 \(\mathbf{S}\)는 MinCutPool의 loss에 중요하게 작용합니다. MinCutPool은 두 가지 loss로 이루어져 있습니다. 첫 번째는 cut loss \(\mathcal{L}_c\), 두 번째는 orthogonality loss \(\mathcal{L}_o\)입니다. \(\mathcal{L}_c\)에 대해서 먼저 확인해보겠습니다.

\[\begin{aligned} \mathcal{L}_c = - \frac{\mathrm{Tr}(\mathbf{S}^{\top} \mathbf{A} \mathbf{S})} {\mathrm{Tr}(\mathbf{S}^{\top} \mathbf{D} \mathbf{S})} \end{aligned}\]

\(\mathcal{L}_c\)는 ‘cluster 내부의 연결성/graph 전체의 연결성’으로, cluster 내부가 전체적인 graph의 연결성과 비교해서 얼마나 끈끈히 연결되어 있는지 알려줍니다. \(\mathrm{Tr}(\mathbf{S}^{\top} \mathbf{A} \mathbf{S})\)이 cluster 내부의 연결성, \(\mathrm{Tr}(\mathbf{S}^{\top} \mathbf{D} \mathbf{S})\)가 graph 전체의 연결성을 나타냅니다. \(\mathbf{D}\)는 \(\mathbf{A}\)의 degree matrix입니다. 예시 code와 함께 살펴봅시다.

import numpy as np
c = [[1, 0, 0],
     [1, 0, 0],
     [1, 0, 0],
     [0, 1, 0],
     [0, 1, 0],
     [0, 1, 0],
     [0, 0, 1],
     [0, 0, 1],
     [0, 0, 1]]

s = [[0.8, 0.2, 0.0],
     [0.8, 0.2, 0.0],
     [0.8, 0.2, 0.0],
     [0.2, 0.6, 0.2],
     [0.2, 0.6, 0.2],
     [0.2, 0.6, 0.2],
     [0.0, 0.1, 0.9],
     [0.0, 0.1, 0.9],
     [0.0, 0.1, 0.9]]

A = [[0 ,1, 1, 0, 0, 0, 0, 0, 0],
     [1 ,0, 1, 0, 0, 0, 0, 0, 0],
     [1 ,1, 0, 0, 0, 1, 0, 0, 1],
     [0 ,0, 0, 0, 1, 1, 0, 0, 0],
     [0 ,0, 0, 1, 0, 1, 0, 0, 0],
     [0 ,0, 1, 1, 1, 0, 0, 0, 1],
     [0 ,0, 0, 0, 0, 0, 0, 1, 1],
     [0 ,0, 0, 0, 0, 0, 1, 0, 1],
     [0 ,0, 1, 0, 0, 1, 1, 1, 0]]

print(np.transpose(c) @ A)
'''
array([[2, 2, 2, 0, 0, 1, 0, 0, 1],
       [0, 0, 1, 2, 2, 2, 0, 0, 1],
       [0, 0, 1, 0, 0, 1, 2, 2, 2]])
- i번째 행, j 번째 열의 원소는 i 번째 cluster와 j 번째 node 사이의 edge 수를 나타냅니다.
- 조금 다르게 생각하면, cluster들이 자신들의 지분이 있는 edge를 챙겨간다고 볼 수도 있습니다.
'''

print(np.transpose(c) @ A @ c)
'''
array([[6, 1, 1],
       [1, 6, 1],
       [1, 1, 6]])
- i번째 행, j 번째 열의 원소는 i 번째 cluster와 j 번째 cluster 사이의 edge 수를 나타냅니다.
- 또 조금 다르게 생각하면 np.transpose(c) @ A에서 챙긴 node별 edge 중, 진짜 자신의 cluster와 
  연결된 edge만을 가져갑니다.
'''

print(np.transpose(s) @ A)
'''
array([[1.6, 1.6, 1.8, 0.4, 0.4, 1.2, 0. , 0. , 1. ],
       [0.4, 0.4, 1.1, 1.2, 1.2, 1.5, 0.2, 0.2, 1. ],
       [0. , 0. , 0.9, 0. , 0. , 0.9, 1.8, 1.8, 1.8]])
- 여섯째 열(node 6)을 기준으로 생각하면, node 6에 연결된 edge 4개를 clsuter red에 1.2개,
  cluster green에 1.5개, cluster blue에 0.9개 분배했습니다.
- node 6에 edge를 제공하던 node는 3, 4, 5, 9번 입니다.
- 그리고 node 3, 4, 5, 9의 cluster별 지분대로 np.transpose(s) @ A 여섯째 열의 원소가 결정됩니다.
'''

print(np.transpose(s) @ A @ s)
'''
array([[4.4 , 2.3 , 0.9 ],
       [2.3 , 2.86, 1.26],
       [0.9 , 1.26, 4.86]])
- np.transpose(c) @ A @ c와 마찬가지로 i번째 행, j번째 열의 원소는 i번째 cluster가
  j번째 cluster와 연결된 edge의 숫자를 나타냅니다.
'''

print(np.trace(np.transpose(s) @ A @ s))
'''
- 따라서 trace를 구하게 되면 i번째 cluster 내부의 edge 수의 합을 구할 수 있습니다.
'''

곱해지는 matrix가 adjacency matrix가 아닌 degree matrix가 되면 오히려 더 간단해집니다. Cluster 별로 edge를 분배하던 것을 넘어, 이제 모든 edge의 sum을 구하게 됩니다.

D = np.diag(np.sum(A, axis=1) # Degree matrix를 생성합니다.

print(np.transpose(s) @ D @ s)
'''
array([[5.44, 2.24, 0.32],
       [2.24, 3.28, 1.68],
       [0.32, 1.68, 6.8 ]])
- 정확한 원리까지는 모르겠지만, np.transpose(s) @ A @ s 보다 조금 더
  전체적인 연결성을 대변하는 듯 합니다.
'''

그렇다면 1번 node의 가중치에 따라서 \(- \frac{\mathrm{Tr}(\mathbf{S}^{\top} \mathbf{A} \mathbf{S})} {\mathrm{Tr}(\mathbf{S}^{\top} \mathbf{D} \mathbf{S})}\)의 값은 어떻게 변화할까요? 정답에 해당하는 [1.0, 0.0, 0.0]부터 [0.0, 1.0, 0.0] 까지 첫 두 개의 원소 값만 조절하면서 비교해보았습니다.

import numpy as np
import matplotlib.pyplot as plt

s = [[0.9, 0.1, 0.0],
     [0.8, 0.2, 0.0],
     [0.8, 0.2, 0.0],
     [0.2, 0.6, 0.2],
     [0.2, 0.6, 0.2],
     [0.2, 0.6, 0.2],
     [0.0, 0.1, 0.9],
     [0.0, 0.1, 0.9],
     [0.0, 0.1, 0.9]]


A = [[0 ,1, 1, 0, 0, 0, 0, 0, 0],
     [1 ,0, 1, 0, 0, 0, 0, 0, 0],
     [1 ,1, 0, 0, 0, 1, 0, 0, 1],
     [0 ,0, 0, 0, 1, 1, 0, 0, 0],
     [0 ,0, 0, 1, 0, 1, 0, 0, 0],
     [0 ,0, 1, 1, 1, 0, 0, 0, 1],
     [0 ,0, 0, 0, 0, 0, 0, 1, 1],
     [0 ,0, 0, 0, 0, 0, 1, 0, 1],
     [0 ,0, 1, 0, 0, 1, 1, 1, 0]]

D = np.diag(np.sum(A, axis=1))

a11 = np.arange(1.0, -1e-5, -0.01)
a12 = np.arange(0.00, 1.0+1e-5, 0.01)
a13 = np.zeros(len(a11))
a1 = np.stack((a11, a12, a13), 1)

result = []
min = 0
min_idx = 0

for i, a in enumerate(a1):
  s[0] = a
  result.append(-np.trace(np.transpose(s) @ A @ s)/np.trace(np.transpose(s) @ D @ s))
  if min>result[i]:
    min = result[i]
    min_idx = i

print(min, a1[min_idx])
'''
-0.8204945376760294 [0.87 0.13 0.  ]
'''
plt.scatter(a11, result)
plt.xlabel('Value of s11')
plt.ylabel('loss')
plt.show()

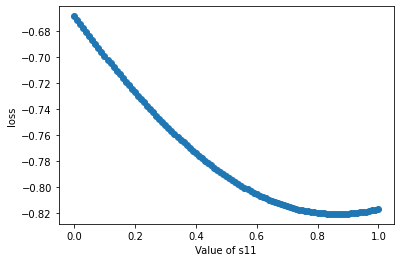
처음에는 loss가 s11의 값이 [1.00, 0.00, 0.00]일 때 최소일 줄 알았는데 꼭 그렇지는 않습니다. 같은 cluster에 속한 다른 node들의 clusterg assignment 값인 [0.80, 0.20, 0.00]과 [1.00, 0.00, 0.00]의 가중 평균 즈음에 해당하는 [0.87 0.13 0.00]에서 최소치를 보입니다. 알다가도 모르겠지만, 정답 cluster에 제대로 접근하는 것과, 같은 cluster내 node 사이의 균형성을 모두 고려하는 듯 합니다. 혹은 3번 node가 node 1, 2와 연결되어 있으니, 실제로 일부 지분은 cluster 2와 cluster 3에 해당할지도 모릅니다. 논문에서 서술한 cut loss의 특성은 다음과 같습니다.

\(\mathcal{L}_c\)는 강하게 연결되어 있는 node가 서로 함께 cluster 되도록 한다고 합니다. \(\mathcal{L}_c\)의 최대값은 0으로, graph 내에 연결된 node가 모두 다른 cluster에 속할 때 최대값에 도달합니다. 최소값은 1로, cluster끼리의 연결이 없으면서 한 cluster내의 node들은 모두 동일하며 다른 cluster와 orthogonal한 \(\mathbf{S}\)를 가질 때 발생합니다. \(\mathcal{L}_c\)는 non-convex한 문제여서 local minima에 갇힐 우려가 있다고 합니다. 예를 들어 모든 node를 한 cluster로 묶거나, 모든 node가 모든 cluster에 균일하게 퍼지는 경우입니다.

s = [[1/3, 1/3, 1/3],
     [1/3, 1/3, 1/3],
     [1/3, 1/3, 1/3],
     [1/3, 1/3, 1/3],
     [1/3, 1/3, 1/3],
     [1/3, 1/3, 1/3],
     [1/3, 1/3, 1/3],
     [1/3, 1/3, 1/3],
     [1/3, 1/3, 1/3]]

print(-np.trace(np.transpose(s) @ A @ s)/np.trace(np.transpose(s) @ D @ s))
'''
-1
'''

s = [[1.0, 0.0, 0.0],
     [1.0, 0.0, 0.0],
     [1.0, 0.0, 0.0],
     [1.0, 0.0, 0.0],
     [1.0, 0.0, 0.0],
     [1.0, 0.0, 0.0],
     [1.0, 0.0, 0.0],
     [1.0, 0.0, 0.0],
     [1.0, 0.0, 0.0]]

print(-np.trace(np.transpose(s) @ A @ s)/np.trace(np.transpose(s) @ D @ s))
'''
-1
'''

MP operation 자체가 node feature를 uniform하게 하는 경향이 있어 이런 local minima에 갇힐 위험이 더욱 올라갑니다. 이럴 때를 대비해서 orthogonality loss가 존재합니다. 이 orthogonality loss에 대한 자세한 정보는 다음 글에서 확인해보도록 하겠습니다.

출처

• Bianchi, Filippo Maria, Daniele Grattarola, and Cesare Alippi. “Spectral clustering with graph neural networks for graph pooling.” In International Conference on Machine Learning, pp. 874-883. PMLR, 2020.
  
• Han, Yufei, and Maurizio Filippone. “Mini-batch spectral clustering.” In 2017 International Joint Conference on Neural Networks (IJCNN), pp. 3888-3895. IEEE, 2017.
  
• Tian, Fei, Bin Gao, Qing Cui, Enhong Chen, and Tie-Yan Liu. “Learning deep representations for graph clustering.” In Proceedings of the AAAI Conference on Artificial Intelligence, vol. 28, no. 1. 2014.